TDBファイルでギブスエネルギーを定義する¶

ギブスエネルギーの定義¶

　TDBファイルにはギブスエネルギーが集録されている。たとえば下記の式（正則溶体モデルによるギブスエネルギー）が記述されている。

(1)¶\[G_{\mathrm{m}}^{\mathrm{BCC}} = x_{\mathrm{A}} {}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-A}} + x_{\mathrm{B}} {}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-B}} + RT \sum_{i=\mathrm{A}}^{\mathrm{B}} x_i \ln{x_i} + x_{\mathrm{A}} x_{\mathrm{B}} L^{(0)}_{\mathrm{A,B}}\]

　このギブスエネルギーを記述するために必要な要素を抽出すると

BCC	相名
$x_{\mathrm{A}}, x_{\mathrm{B}}$	構成元素
${}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-A}}, {}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-B}}$	純物質のギブスエネルギー
$L^{(0)}_{\mathrm{A,B}}$	相互作用パラメータ

TDBの構造¶

 $ ------------------------------------------------------------------
 $
 $ A-B二元系状態図
 $ TDBファイルの記述例
 $-------------------------------------------------------------------
 ELEMENT   A   BCC    10    0    0 !
 ELEMENT   B   BCC    20    0    0 !
　$
 FUNCTION  RR     300  +8.3145;                6000 N !
FUNCTION  GBCCA  300  -1000*RR+RR*T;          6000 N !
FUNCTION  GBCCB  300  -2000*RR+RR*T;          6000 N !
12
TYPE_DEFINITION % SEQ * !
14
PHASE LIQUID:L % 1  1  !
CONSTITUENT LIQUID : A,B : !
PARAMETER  G(LIQUID,A;0)    300  +0;           6000 N !
PARAMETER  G(LIQUID,B;0)    300  +0;           6000 N !
PARAMETER  G(LIQUID,A,B;0)  300  -10000;       6000 N !
20
PHASE BCC % 1  1  !
CONSTITUENT BCC : A,B : !
PARAMETER  G(BCC,A;0)    300  -1000*RR+RR*T;   6000 N !
PARAMETER  G(BCC,B;0)    300  -2000*RR+RR*T;   6000 N !
PARAMETER  G(BCC,A,B;0)  300  -5000;           6000 N !

１〜５行目	ヘッダー
６、７行目	元素の定義
９〜１１行目	関数の定義
１３行目	Type-definition
１５、１６行目	液相の定義
１７〜１９行目	パラメータの定義

仮想A-B二元系のTDB¶

　仮想A-B二元系を例に、TDBファイルの基本的な記述ルールについて、実際に入力しながら説明します。テキストエディタを立ち上げて、赤字の部分をタイプしてください。

注釈

タブは使わないでください（スペースのみ）。

ヘッダー¶

$--------1---------2---------3---------4---------5---------6---------7---------8
$
$ 「ＴＤＢファイルの作り方」説明用テストファイル           2011.12.7
$
$ 　物質・材料研究機構　理論計算科学ユニット　阿部太一
$
$ Particle Simulation and Thermodynamics Group, National Institute for
$ Materials Science. 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan
$ e-mail: abe.taichi @ nims.go.jp        Copyright(C)Taichi ABE 2010
$-------------------------------------------------------------------------------

“$”で始まる行はコメント行。 Thermo-Calcは一行に80文字までしか書けない。PANDATはそれ以上でもOK。

元素の定義¶

　定義には ELEMENT コマンドを使う。

ELEMENT   A   BCC    10    0    0 !　　　$ PANDATは途中からもコメントを入れられる
ELEMENT   B   BCC    20    0    0 !
ELEMENT   VA  VAC     0    0    0 !

各値の意味は左から

元素記号（二文字まで、仮想元素有）
安定結晶構造
原子量
標準状態でのエンタルピー
エントロピー

安定結晶構造は、標準状態における最安定結晶構造

“！”はこのコマンドの終わりを意味している。全てのコマンドの最後には必ずつけること。

関数の定義¶

　定義には FUNCTION コマンドをを使う。

FUNCTION  RR      300   +8.3145;    6000  N !

　各値の意味は左から、

関数名
関数が有効な温度下限
実際の関数（；は関数の終了を表す。）
関数が有効な温度上限
さらに高温側に関数を定義するかどうか（Y/Ｎ）
！はこのコマンドの終了

FUNCTION  RRR     300   +8.3145;   　　　　　　　　2000  Y
                  　　　+500*T*LN(T); 　  　　　　 5000  Y
　　　　　　　　　　　　+150E-10-50*T**(-2);       6000  N !

　この例では300 Kから6000 Kの間に3つの関数が定義されている。

　このように関数の定義は低温側から高温側の順で行う。

Type-definition¶

　下の三行がないとThermo-Calcは動かない。Ｔｈｅｒｍｏ－ｃａｌｃ以外では不要。

TYPE_DEFINITION　　 %　　 SEQ　　 *　!

　 % で、 SEQ　　 * を呼び出すように設定している。

注釈

ＴＣでデータを出力すると自動的に下記の二行が加えられる。詳細はテキスト参照。

DEFINE_SYSTEM_DEFAULT  ELEMENT  2  !
DEFAULT_COMMAND  DEF_SYS_ELEMENT  VA  /- !

ＭａｔｃａｌｃではＶａの定義が必須。

Type-definitionは、磁気過剰ギブスエネルギーの定義やCEFの定義などに必要なので、相の定義の後でまた取り上げます。

相の定義¶

　定義には PHASE コマンドを使う。

PHASE 　BCC　 % 　1 　 1 　 !

　各値の意味は左から、

定義する相名
Type-definitionの呼び出し（TYPE_DEFINITION % SEQ *　!）
副格子の数
第一副格子上の格子点の数
定義の終了

成分の定義¶

　定義には CONSTITUENT コマンドを使う。

CONSTITUENT BCC 　: A,B : 　!

　各値の意味は左から、

対象とする相
副格子の区切り
第一副格子上の構成成分
副格子の区切り
定義の終了

パラメーターの定義¶

　定義には PARAMETER コマンドを使う。　BCC相のギブスエネルギーを下記の式で記述した場合、

\[G_{\mathrm{m}}^{\mathrm{BCC}} = x_{\mathrm{A}} {}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-A}} + x_{\mathrm{B}} {}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-B}} + RT \sum_{i=\mathrm{A}}^{\mathrm{B}} x_i \ln{x_i} + x_{\mathrm{A}} x_{\mathrm{B}} L^{(0)}_{\mathrm{A,B}}\]

　成分純Aのギブスエネルギー ${}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-A}}$ は、

PARAMETER   G(BCC,A;0)      300   +GBCCA;   6000   N   !

　各値の意味は左から、

BCC構造の成分Aのギブスエネルギー（G）
R-K級数のn=0項
温度範囲下限
関数
温度範囲上限

純物質の関数は複雑なので、多くの場合関数は別途定義しておく。

　同様に成分純Bのギブスエネルギー ${}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-B}}$ は、

PARAMETER G(BCC,B;0)      300    +GBCCB;   6000 N !

　相互作用パラメータ $L^{(0)}_{\mathrm{A,B}}$ のR-K級数n=0項

PARAMETER G(BCC,A,B;0)    300    -5000;    6000 N !

　純物質A、Bのギブスエネルギー関数を定義する。

FUNCTION  GBCCA    300   -1000*RR+RR*T; 6000 N !
FUNCTION  GBCCB    300   -2000*RR+RR*T; 6000 N !

LIQUIDの定義¶

　BCC相と同様に液相のギブスエネルギー式を入力(副格子がない場合)する。

(2)¶\[G_{\mathrm{m}}^{\mathrm{Liq}} = x_{\mathrm{A}} {}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{Liq-A}} + x_{\mathrm{B}} {}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{Liq-B}} + RT \sum_{i=\mathrm{A}}^{\mathrm{B}} x_i \ln{x_i} + x_{\mathrm{A}} x_{\mathrm{B}} [L^{(0)}_{\mathrm{A,B}} + L^{(1)}_{\mathrm{A,B}}(x_{\mathrm{A}} - x_{\mathrm{B}}) + L^{(2)}_{\mathrm{A,B}}(x_{\mathrm{A}} - x_{\mathrm{B}})^2 ]\]

　純物質のギブスエネルギーと過剰ギブスエネルギーを下記のように記述する。相互作用パラメータについては、R-K級数n=0,1,2項 $L^{(0)}_{\mathrm{A,B}}$ 、 $L^{(1)}_{\mathrm{A,B}}$ 、 $L^{(2)}_{\mathrm{A,B}}$ の３つを使用している。

PHASE LIQUID  %   1  1  !
CONSTITUENT LIQUID　：  A,B ： !
PARA  G(LIQUID,A;0)    300  +GLIQA;         6000  N !
PARA  G(LIQUID,B;0)    300  +GLIQB;         6000  N !
PARA  G(LIQUID,A,B;0)  300  +L0;  　　　　   6000  N !
PARA  G(LIQUID,A,B;1)  300  +L1; 　　　　    6000  N !
PARA  G(LIQUID,A,B;2)  300  +L2;    　　　　 6000  N !

注釈

アルファベット順に注意TCではOKだが、Pandatでは逆に解釈される

TDBファイルの完成形¶

$ ------------------------------------------------------------------
$
$ A-B二元系状態図    　　　阿部太一　2015.7.1
$ TDBファイルの記述例
$-------------------------------------------------------------------
ELEMENT   A   BCC    10    0    0 !
ELEMENT   B   BCC    20    0    0 !
ELEMENT   VA  VAC     0    0    0 !

FUNCTION RR     300   +8.3145;                 6000 N !
FUNCTION GBCCA  300  -1000*RR+RR*T;            6000 N !
FUNCTION GBCCB  300  -2000*RR+RR*T;            6000 N !

TYPE_DEFINITION % SEQ * !

PHASE LIQUID   % 1  1  !
CONSTITUENT LIQUID : A,B : !
PARAMETER  G(LIQUID,A;0)    300  +0;           6000 N !
PARAMETER  G(LIQUID,B;0)    300  +0;           6000 N !
PARAMETER  G(LIQUID,A,B;0)  300  -10000;       6000 N !

PHASE BCC % 1  1  !
CONSTITUENT BCC : A,B : !
PARAMETER  G(BCC,A;0)    300  +GBCCA;          6000 N !
PARAMETER  G(BCC,B;0)    300  +GBCCB;          6000 N !
PARAMETER  G(BCC,A,B;0)  300  -5000;           6000 N !

状態図を計算させてみましょう¶

　ファイルの拡張子はtdbにしてください。

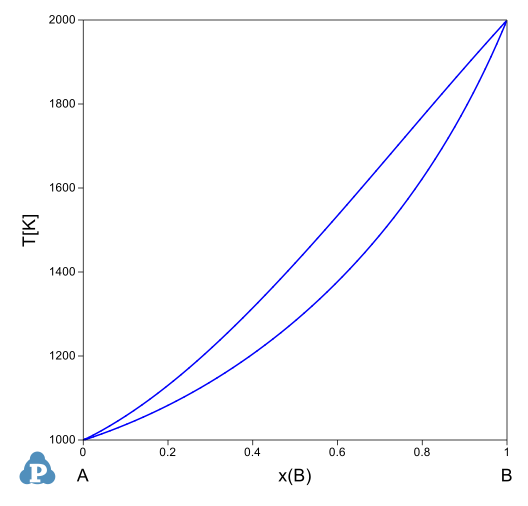
仮想A-B-C三元系のTDB¶

ELEMENT   A   BCC    10    0    0 !
ELEMENT   B   BCC    20    0    0 !
ELEMENT   VA  VAC     0    0    0 !
ELEMENT   C   BCC    20    0    0 !

FUNCTION RR     300   +8.3145;                 6000 N !
FUNCTION GBCCA  300  -1000*RR+RR*T;            6000 N !
FUNCTION GBCCB  300  -2000*RR+RR*T;            6000 N !
FUNCTION GBCCC  300  -500*RR+RR*T;             6000 N !

TYPE_DEFINITION % SEQ * !

PHASE LIQUID   % 1  1  !
CONSTITUENT LIQUID : A,B,C : !
PARAMETER  G(LIQUID,A;0)      300  +0;           6000 N !
PARAMETER  G(LIQUID,B;0)      300  +0;           6000 N !
PARAMETER  G(LIQUID,C;0)      300  +0;           6000 N !
PARAMETER  G(LIQUID,A,B;0)    300  -10000;       6000 N !
PARAMETER  G(LIQUID,A,B,C;0)  300  -10000;       6000 N !
PARAMETER  G(LIQUID,A,B,C;1)  300  -10000;       6000 N !
PARAMETER  G(LIQUID,A,B,C;2)  300  -10000;       6000 N !

三元系の相互作用パラメータ¶

(3)¶\[G_{\mathrm{m}}^{\mathrm{Excess-ter}} = x_{\mathrm{A}} x_{\mathrm{B}} x_{\mathrm{C}} [ x_{\mathrm{A}} L^{(0)}_{\mathrm{A,B,C}} + x_{\mathrm{B}} L^{(1)}_{\mathrm{A,B,C}} + x_{\mathrm{C}} L^{(2)}_{\mathrm{A,B,C}}]\]

BCCの定義¶

PHASE BCC % 1  1  !
CONSTITUENT BCC : A,B,C : !
PARAMETER  G(BCC,A;0)    300  +GBCCA;          6000 N !
PARAMETER  G(BCC,B;0)    300  +GBCCB;          6000 N !
PARAMETER  G(BCC,C;0)    300  +GBCCC;          6000 N !
PARAMETER  G(BCC,A,B;0)  300  -5000;           6000 N !

1000Kにおける等温断面¶

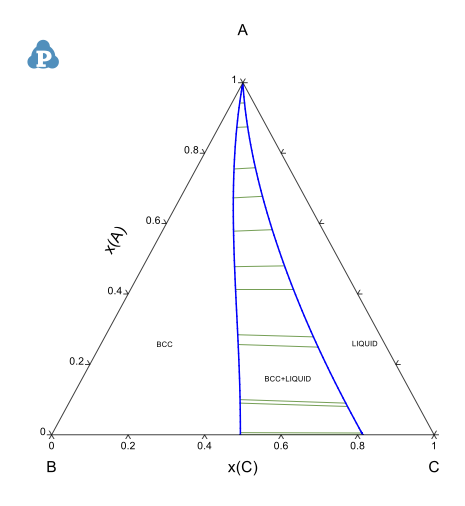
タイラインを表示するには、図をクリック⇒Property⇒Tieline property

記述ルールまとめ¶

コメント文
“$”はその行がコメント文であることを意味している。PANDATでは式の途中からコメントを加えることができる。日本語でもよい（文字化けするがエラーにはならない）。
最大文字数
Thermo-Calcでは、一行に書くことができる最大の文字数が80文字と決まっている。ほかのソフトウェアでは、一行の文字数制限はない.ただし改行した時には一文字目を空白にすること。
定義式の終了
すべての定義式の最後には“!”を付ける。付いていないと次の行まで定義式が続いていると解釈される。
空白行
空白行はそのままスキップされる。
記述の短縮
たとえば元素を定義する6行目のELEMENTは、ELEMやELEと短縮できる。ほかの定義も、その定義がほかの定義と区別できる長さまで短縮できる。ELEMENTの場合、たとえばほかにEで始まる定義がなければ、Eと表記すればよいが、ENTERラインによる定義があるためELEMENTに対してはそれらと区別できるELが最短の形式となる。
パラメーターの単位
TDBファイルではSI単位を用いる。ギブスエネルギーG [J/mol]、圧力 P [Pa]、温度T [K]である。[mol]は原子１モル、または分子・化合物１モルが用いられている。
元素の並び順
Redlich-Kister(R-K)級数項の記述において、副格子中の成分は常にアルファベット順で記述すること。G(SOLID,B,A;0)ではなく、G(SOLID,A,B;0)と記述すること。Thermo-Calcではどちらの記述も同じ意味になるが、PANDATとCaTCalcでは、アルファベット順を逆にすると、R-K級数の奇数項は符号が逆転する。
大文字と小文字
Thermo-Calcでは、関数名や相名は小文字で記述するとエラーとなる。そのほかの記述でも小文字が混ざっていることでエラーが現れることがある。また、ソフトウェアやバージョンにも依存するため、TDBファイルはすべて大文字で記述すること。
演算記号
割り算記号”/”は用いることができない。たとえばA/Tではなく、A*T**(-1)

注釈

すべて大文字、アルファベット順で書く

副格子の定義¶

　BCC相に空の侵入型副格子を追加する。

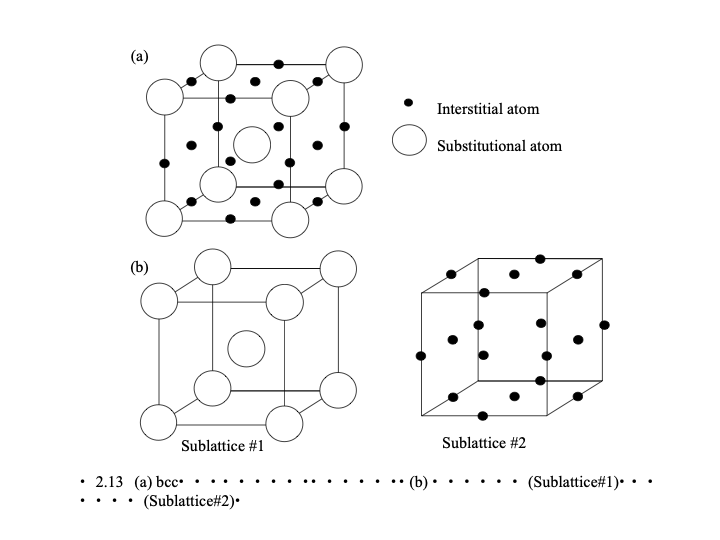
副格子を分ける¶

　元々のBCC相のギブスエネルギーの定義は以下のように記述されていた。

PHASE BCC % 1  1  !
CONSTITUENT BCC : A,B : !
PARAMETER  G(BCC,A;0)    300  -1000*RR+RR*T;   6000 N !
PARAMETER  G(BCC,B;0)    300  -2000*RR+RR*T;   6000 N !
PARAMETER  G(BCC,A,B;0)  300  -5000;           6000 N !

　これを以下のように修正する。

PHASE BCC % 2  1  3 !
CONSTITUENT BCC : A,B : VA :!
PARAMETER  G(BCC,A:VA;0)    300  -1000*RR+RR*T;   6000 N !
PARAMETER  G(BCC,B:VA;0)    300  -2000*RR+RR*T;   6000 N !
PARAMETER  G(BCC,A,B:VA;0)  300  -5000;           6000 N !

PHASE の副格子の数を１から2へ変更する。侵入型副格子はBCCの八面体サイトなので、第一副格子は１モルに対し、第二副格子は3モルとなる。
CONSTITUENT に第二副格子の構成成分としてVA（空孔のみ）を加える。
PARAMETER にもVAを加える。

A-B二元系に化合物を加える¶

　相名はA2B3とする。２副格子に分け、副格子＃１は元素A、副格子＃２は元素Bが占める。

PHASE A2B3   %   2   2   3  !
CONSTITUENT  A2B3   :  A :  B  : !
PARAMETER  G(A2B3,A:B;0)    300    +2*GBCCA+3*GBCCB-50000;    6000  N !

　これは化合物を１モルとした記述で、原子のモル数は 2 + 3 = 5モルになる。

　一方、下記は原子数を１モルとした記述であり、生成ギブスエネルギーは1/5になる。

PHASE A2B3   %    2    0.4    0.6  !
CONSTITUENT  A2B3   :  A  :  B  : !
PARAMETER  G(A2B3,A:B;0)    300     +0.4*GBCCA+0.6*GBCCB-10000;    6000  N !

化合物を加えたAB二元系状態図¶

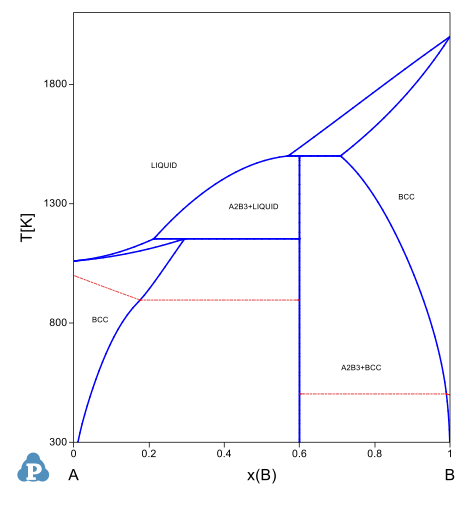
このような手順で、C-Feなどの実際の合金系のTDBを作成してみましょう。

TDBファイルでギブスエネルギーを定義する¶

ギブスエネルギーの定義¶

TDBの構造¶

仮想A-B二元系のTDB¶

ヘッダー¶

元素の定義¶

関数の定義¶

Type-definition¶

相の定義¶

成分の定義¶

パラメーターの定義¶

LIQUIDの定義¶

TDBファイルの完成形¶

状態図を計算させてみましょう¶

仮想A-B-C三元系のTDB¶

三元系の相互作用パラメータ¶

BCCの定義¶

1000Kにおける等温断面¶

記述ルールまとめ¶

副格子の定義¶

副格子を分ける¶

A-B二元系に化合物を加える¶

化合物を加えたAB二元系状態図¶

目次

前のトピックへ

BCC	相名
\(x_{\mathrm{A}}, x_{\mathrm{B}}\)	構成元素
\({}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-A}}, {}^{\mathrm{o}}G_{\mathrm{m}}^{\mathrm{BCC-B}}\)	純物質のギブスエネルギー
\(L^{(0)}_{\mathrm{A,B}}\)	相互作用パラメータ