calculate, equilibrium を使って熱力学計算¶
状態図の計算には、
熱力学パラメータから全ての相のギブスエネルギーの計算(正則溶体近似)
平衡状態(無限に時間をおいた場合に到達する最もエネルギーが低い状態)の計算
の2つを行なっています。
binplot では、1について Calculate を、2について equilibrium を使って、さまざまな温度、組成での状態図の計算を行っています。Calculate を使うと、指定した相のギブスエネルギー(他の物性値を含む)を計算することができます。また equilibrium を使うと、複数の相が関わる平衡状態を計算することができます。
ここでは、 Al-Zn 2元系を用いて Calculate と equilibrium の計算結果について説明します。
Al-Zn (S. Mey, 1993)¶
Al-Zn 状態図には、高温の液相(L)、Al側のFCC相、Zn側のHCP相が単相として現れており、それ以外は二相領域となっています。FCC相の温度277℃、Zn濃度16.5 ~ 59.0%には溶解度ギャップが含まれています。
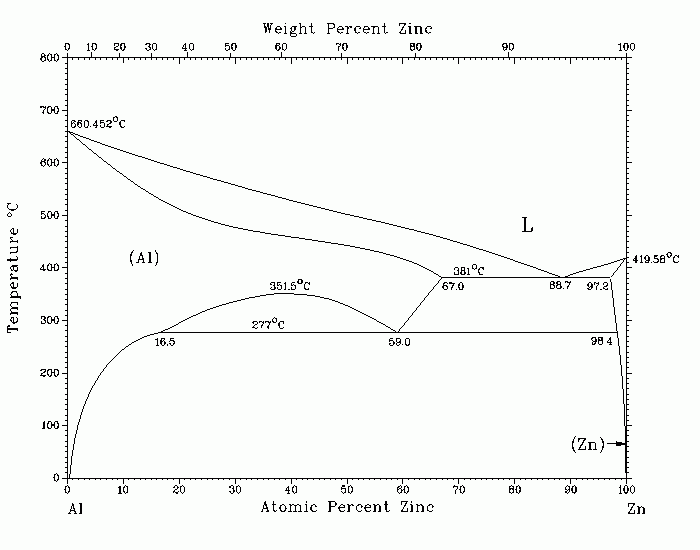
参考文献:S. an Mey, Zeitschrift für Metallkunde 84(7) (1993) 451-455.
必要なライブラリとデータベースを読み込みます。
[1]:
%matplotlib inline
from pycalphad import Database, calculate, equilibrium, variables as v
dbf = Database('alzn_mey.tdb')
comps = ['AL', 'ZN', 'VA']
次に考慮する相を選択します。 alzn_mey.tdbにどのような相が含まれているか確かめるには、メモ帳などのテキストエディタで alzn_mey.tdbを開き、PHASE で始まっている行を確認してください。LinuxかMacを使っている場合には、以下のようにしても相の情報が得られます。
[2]:
!grep PHASE alzn_mey.tdb
alzn_mey.tdbにはLIQUID、FCC_A1、HCP_A3相が含まれています。これらの相をphases_alznとして取り込むには以下のようにします。
[3]:
phases_alzn = ['LIQUID', 'FCC_A1', 'HCP_A3']
calculate()¶
calculate は、指定した相の物性値を計算するために使用します。実行する際、4つの引数を指定する必要があります。
calculate(database, components, phases, Pressure, Temperature)`
例えば1気圧(1013125 Pa)、\(T\) = 500 K ~ 1100 Kの間を100 Kステップで計算するには以下のようにします。
calculate(dbf, comps, phase, P=101325, T=(500, 1100, 100))
データ構造¶
pycalphadにおいて、 calculate または equilibrium で行った計算結果は、xarray データセットとして返されます。xarray データセットは N 次元の表形式のデータ構造です。 これは、Pandas DataFrame の N 次元版とよく似ています。xarray データセットの詳細なドキュメントとチュートリアルは、xarray ドキュメント を参照してください。
xarray データセット¶
ここでは、pycalphad の xarray データセットの構造とその基本的な使用法について説明します。各データセットには、計算条件と物性値が格納されます。 3 つの重要な用語があります。
Dimensions: 圧力(P)、温度(T)などがDimensions(次元)として用いられます。Coordinates:Dimensionsのラベルです。Data variables: ギブスエネルギー、混合エネルギー、組成など、pycalphad によって計算される物性値です。
pandasにはない概念として、DatasetやDataArrayの各次元軸を規定する dimension(s) があります。 Dimensionsは軸名と軸の値を持つラベルとして、1次元のDataArrayで表現されます。 これらは、coordinatesとは別に生成することもできますし、1次元のcoordinatesを割り当てることもできます。これらの概念をpandasとの比較でまとめると以下の通りです。
xarray |
pandas |
|
|---|---|---|
次元軸 |
Dimension(s) (xr.DataArray) |
n/a |
ラベル |
Coordinate(s) (xr.DataArray) |
(Multi)Index (pd.(Multi)Index) |
データ |
DataArray (xr.DataArray) |
Series (pd.Series) |
データセット |
Dataset (xr.Dataset) |
DataFrame (pd.DataFrame) |
dimensions/coordinates¶
計算時に5つのdimensions/coordinatesをもつxarrayデータセットがつくられます。
component: 構成元素N: 全原子数 (mol)(1に固定されるため数えない)P: 圧力 (Pa)T: 温度 (K)points: 計算点。デフォルトですべての内部自由度にわたって計算点をサンプリングします。pointsには物理的な意味や順序はありません。internal_dof: 内部自由度。FCC_A1相の副格子モデル(AL、ZN)の場合には、internal_dof はALサイトの0、ZN サイトの1です。
データ変数¶
Calculate によって出力される計算結果には 4 つのデータがあります。
Phase: 相X: モル分率で表した各成分の組成(温度、圧力、計算点の関数)Y:inner_dof配列内の各インデックスの サイトフラクション (温度、圧力、計算点の関数)output: 物性値(デフォルトはモルギブズエネルギーGM)
Calculate を使って、FCC_A1相の物性値を計算するには以下のようにします。
[4]:
calc_result = calculate(dbf, comps, 'FCC_A1', P=101325, T=(500, 1100, 100))
print(calc_result)
<xarray.Dataset>
Dimensions: (N: 1, P: 1, T: 6, points: 4001, component: 2, internal_dof: 2)
Coordinates:
* component (component) <U2 'AL' 'ZN'
* N (N) float64 1.0
* P (P) float64 1.013e+05
* T (T) float64 500.0 600.0 700.0 800.0 900.0 1e+03
Dimensions without coordinates: points, internal_dof
Data variables:
X (N, P, T, points, component) float64 1.0 1e-14 ... 0.7439 0.2561
Phase (N, P, T, points) <U6 'FCC_A1' 'FCC_A1' ... 'FCC_A1' 'FCC_A1'
Y (N, P, T, points, internal_dof) float64 1.0 1e-14 ... 0.2561
GM (N, P, T, points) float64 -1.559e+04 -2.01e+04 ... -4.81e+04
Attributes:
phase_indices: {'FCC_A1': slice(0, 4001, None)}
/Users/iikubo/miniconda3/lib/python3.9/site-packages/pycalphad/core/utils.py:54: RuntimeWarning: invalid value encountered in divide
pts[:, cur_idx:end_idx] /= pts[:, cur_idx:end_idx].sum(axis=1)[:, None]
計算結果を操作する¶
計算結果のxarrayデータセット(ここでは calc_result )を操作するには、coordinates(座標)を使って抽出します。
Pandas 配列と同様に、selを使用して座標値でデータを選択するか、iselを使用して座標のインデックスでデータを選択します。
適切にデータ変数を選択することで、プロットや計算の実行に役立つ xarray データセットを得ることができます。
例えば、calc_result におけるサイトフラクションY のうち、
ZNのサイト (internal_dof = 1)
50 番目の計算点
500 K
を取得するには以下のようにします。
[5]:
print(calc_result.Y.isel(internal_dof=1, points=49).sel(T=500))
<xarray.DataArray 'Y' (N: 1, P: 1)>
array([[0.97648824]])
Coordinates:
* N (N) float64 1.0
* P (P) float64 1.013e+05
T float64 500.0
DataArray の values 属性にアクセスすると、多次元 NumPy 配列が返されます
[6]:
print(calc_result.Y.isel(internal_dof=1, points=49).sel(T=500).values)
[[0.97648824]]
計算結果から500 KのZnの組成ZNを得るには以下のようにします。
[7]:
print(calc_result.X.sel(component='ZN').sel(T=500).values)
[[[1.00000000e-14 1.00000000e+00 1.00000000e+00 ... 8.43004350e-01
8.87927218e-01 2.56066359e-01]]]
計算結果から500 KのモルギブスエネルギーGM を得るには以下のようにします。
[8]:
print(calc_result.GM.sel(T=500).values)
[[[-15589.38872794 -20099.46240961 -20099.46240961 ... -20683.03658045
-20722.47948049 -17338.16556129]]]
計算によって得られたギブスエネルギーを図示します。
[9]:
import matplotlib.pyplot as plt
plt.scatter(calc_result.X.sel(component='ZN'), calc_result.GM, marker='.')
[9]:
<matplotlib.collections.PathCollection at 0x14679bfa0>
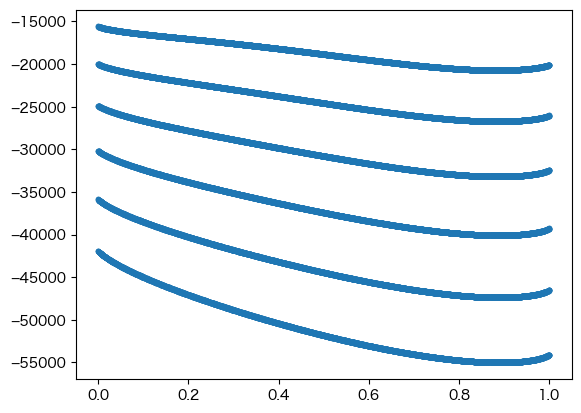
軸タイトルや凡例は以下のようにつけます。
[10]:
import matplotlib.pyplot as plt
from pycalphad.plot.utils import phase_legend
# Get the colors that map phase names to colors in the legend
legend_handles, color_dict = phase_legend(phases_alzn)
fig = plt.figure(figsize=(6,4))
ax = fig.gca()
ax.scatter(calc_result.X.sel(component='ZN'), calc_result.GM, marker='.')
# Format the plot
ax.set_xlabel('X(Zn)')
ax.set_ylabel('GM (J/mol)')
ax.set_xlim((0, 1))
ax.set_ylim((-60000, 0))
ax.legend(handles=legend_handles, loc='upper right')
plt.show()
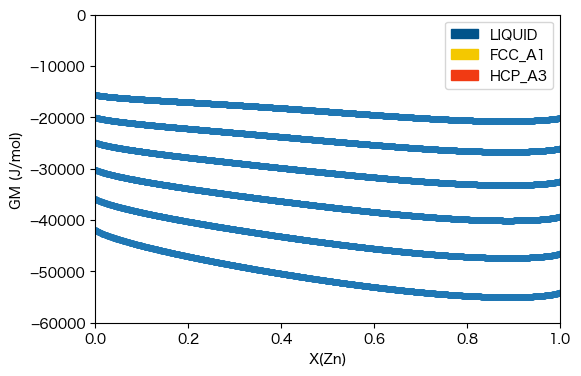
\(T\) = 500 Kで3つの相(LIQUID、FCC_A1、HCP_A3)のギブスエネルギーを比較するには以下のようにします。
[11]:
import matplotlib.pyplot as plt
from pycalphad.plot.utils import phase_legend
# Get the colors that map phase names to colors in the legend
legend_handles, color_dict = phase_legend(phases_alzn)
fig = plt.figure(figsize=(6,4))
ax = fig.gca()
# Loop over phases, calculate the Gibbs energy, and scatter plot GM vs. X(RE)
for phase_name in phases_alzn:
result = calculate(dbf, comps, phase_name, P=101325, T=500, output='GM')
ax.scatter(result.X.sel(component='ZN'), result.GM, marker='.', s=5, color=color_dict[phase_name])
# Format the plot
ax.set_xlabel('X(Zn)')
ax.set_ylabel('GM (J/mol)')
ax.set_xlim((0, 1))
ax.legend(handles=legend_handles, loc='upper right')
plt.show()
/Users/iikubo/miniconda3/lib/python3.9/site-packages/pycalphad/core/utils.py:54: RuntimeWarning: invalid value encountered in divide
pts[:, cur_idx:end_idx] /= pts[:, cur_idx:end_idx].sum(axis=1)[:, None]
/Users/iikubo/miniconda3/lib/python3.9/site-packages/pycalphad/core/utils.py:54: RuntimeWarning: invalid value encountered in divide
pts[:, cur_idx:end_idx] /= pts[:, cur_idx:end_idx].sum(axis=1)[:, None]
/Users/iikubo/miniconda3/lib/python3.9/site-packages/pycalphad/core/utils.py:54: RuntimeWarning: invalid value encountered in divide
pts[:, cur_idx:end_idx] /= pts[:, cur_idx:end_idx].sum(axis=1)[:, None]
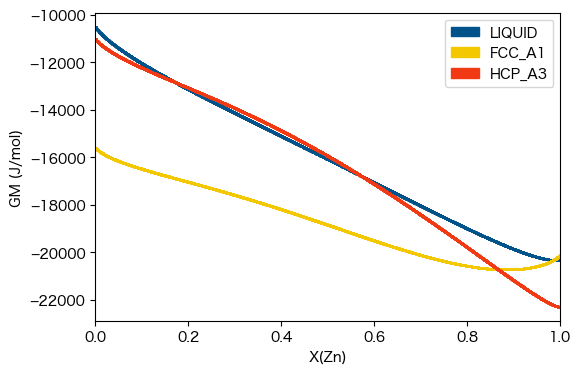
equilibrium()¶
equilibrium を使うと、複数の相が関わる平衡状態における物性値を計算することができます。
実行する際には、以下のように4つの引数を指定する必要があります。
equilibrium(database, components, phases, conditions, output)
例えば1気圧(1013125 Pa)、\(T\) = 500 K ~ 1000 Kの間を100 Kステップ、HM(モルエンタルピー)を計算するには以下のようにします。
equilibrium(dbf, comps , phases, {v.X('ZN'):(0,1,0.05), v.T: (500, 1000, 100), v.P:101325}, output='HM')
[12]:
phases = ['LIQUID', 'FCC_A1', 'HCP_A3']
eq_result = equilibrium(dbf, comps , phases, {v.X('ZN'):(0,1,0.05), v.T: (500, 1000, 100), v.P:101325}, output='HM')
print(eq_result)
<xarray.Dataset>
Dimensions: (N: 1, P: 1, T: 5, X_ZN: 20, vertex: 3, component: 2,
internal_dof: 2)
Coordinates:
* N (N) float64 1.0
* P (P) float64 1.013e+05
* T (T) float64 500.0 600.0 700.0 800.0 900.0
* X_ZN (X_ZN) float64 1e-10 0.05 0.1 0.15 0.2 ... 0.75 0.8 0.85 0.9 0.95
* vertex (vertex) int64 0 1 2
* component (component) <U2 'AL' 'ZN'
Dimensions without coordinates: internal_dof
Data variables:
NP (N, P, T, X_ZN, vertex) float64 1.0 nan nan 1.0 ... 1.0 nan nan
GM (N, P, T, X_ZN) float64 -1.559e+04 -1.615e+04 ... -5.068e+04
MU (N, P, T, X_ZN, component) float64 -1.559e+04 ... -5.065e+04
X (N, P, T, X_ZN, vertex, component) float64 1.0 1e-10 ... nan nan
Y (N, P, T, X_ZN, vertex, internal_dof) float64 1.0 1e-10 ... nan
Phase (N, P, T, X_ZN, vertex) <U6 'FCC_A1' '' '' ... 'LIQUID' '' ''
HM (N, P, T, X_ZN) float64 5.194e+03 5.859e+03 ... 2.528e+04
Attributes:
engine: pycalphad 0.10.2
created: 2025-03-16T21:52:24.218917
dimensions/coordinates¶
equilibrium() データセットには、6 つの dimensions/coordinates があります。
N: 全原子数 (mol)P: 圧力 (Pa)T: 温度 (K)X_ZN:conditionsに渡された元素の組成(うえではv.X('ZN')としたのでX_ZN)vertex:vertex(頂点)は、平衡状態に含まれる相のインデックス
vertex自体には物理的な意味はなく、平衡状態に含まれる相を記述するのに十分な数がギブスの相律従い自動的生成される。
component: 系に含まれる元素internal_dof: 内部自由度、任意の相のサイトフラクション配列内のインデックス
FCC_A1相の副格子モデル(AL、ZN)の場合には、internal_dof は整数 0 と 1(ALサイト(0)とZN サイト(1)です。
データ変数¶
equilibrium() によって返されるデータセットは calculate に似ています。データ変数は以下の 6 つです。
Phase: 相
Phaseの数は len(vertex) 個あります。vertexで記述されるインデックスよりも平衡状態にあるPhaseの数が少ない場合、Phaseの値には「』』」が入力されます。例えばFCC_A1 の単相領域の場合、相の値は ['FCC_A1', ''] になります。複数の相が存在する場合、それらは必ずしもソートされていないことに注意してください。
NP: 相分率
相が存在しない場合 NP の値は 0 ではなく nan になります (例: 単相 ['FCC_A1', ''])。
MU: 各成分の化学ポテンシャルX: 各相の平衡組成Y: 各相における各サイトの占有率GM: ギブスエネルギー
calculateのoutputと同じです。 outputの値に関係なく、常に出力されます。
output: (optional) 計算したい平衡状態の物性値
equilibrium()はGMを常に出力するため、outputに設定した物性値はGMに追加されます。
計算結果を操作する¶
例として、\(T\) = 800 K におけるFCC_A1 相の相分率を組成の関数として求めてみましょう。相分率の値にアクセスするには、coodinates(座標)のインデックス、または値が必要になります。
FCC_A1 相を指定する際に、以下のような指定の仕方をするとエラーが起きます。
print(eq_result.NP.sel(Phase='FCC_A1', T=800))
これは、Phaseが dimension/coordinate ではなくデータ変数であるためです。
sel または isel コマンドを使用するには、FCC_A1 相がデータ変数として格納されているセルのインデックスが必要です。
これをひとつひとつ調べることは面倒な作業である。xarrayに備わっているマスキング masking を利用すれば、条件に一致するデータ値を見つけることができます。
データ変数にFCC_A1相が格納されているセルの相分率を表示するには以下のようにします。
[13]:
print(eq_result.NP.where(eq_result.Phase=='FCC_A1'))
<xarray.DataArray 'NP' (N: 1, P: 1, T: 5, X_ZN: 20, vertex: 3)>
array([[[[[1. , nan, nan],
[1. , nan, nan],
[0.97607896, nan, nan],
[0.92129859, nan, nan],
[0.86651821, nan, nan],
[0.81173783, nan, nan],
[0.75695745, nan, nan],
[0.70217707, nan, nan],
[0.64739669, nan, nan],
[0.59261631, nan, nan],
[0.53783594, nan, nan],
[0.48305556, nan, nan],
[0.42827518, nan, nan],
[0.3734948 , nan, nan],
[0.31871442, nan, nan],
[0.26393404, nan, nan],
[0.20915367, nan, nan],
[0.15437329, nan, nan],
[0.09959291, nan, nan],
[0.04481253, nan, nan]],
...
[[1. , nan, nan],
[0.75935221, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan]]]]])
Coordinates:
* N (N) float64 1.0
* P (P) float64 1.013e+05
* T (T) float64 500.0 600.0 700.0 800.0 900.0
* X_ZN (X_ZN) float64 1e-10 0.05 0.1 0.15 0.2 ... 0.75 0.8 0.85 0.9 0.95
* vertex (vertex) int64 0 1 2
次にデータ変数にFCC_A1相が格納されているセルのうち、\(P\) = 101325 Pa, \(T\) = 800 Kの相分率を表示するには以下のようにします。
[15]:
print(eq_result.NP.where(eq_result.Phase=='FCC_A1').sel(P=101325, T=800))
<xarray.DataArray 'NP' (N: 1, X_ZN: 20, vertex: 3)>
array([[[1. , nan, nan],
[1. , nan, nan],
[1. , nan, nan],
[1. , nan, nan],
[0.89739922, nan, nan],
[0.71825009, nan, nan],
[0.53910096, nan, nan],
[0.35995184, nan, nan],
[0.18080271, nan, nan],
[ nan, 0.00165358, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan]]])
Coordinates:
* N (N) float64 1.0
P float64 1.013e+05
T float64 800.0
* X_ZN (X_ZN) float64 1e-10 0.05 0.1 0.15 0.2 ... 0.75 0.8 0.85 0.9 0.95
* vertex (vertex) int64 0 1 2
ここまで行なったことに基づいて、\(T\) = 800 Kにおいて、FCC_A1 相の相分率がZn濃度(X(ZN))に対して変化する図を作りましょう。
まずx軸に対応するZn濃度(X(ZN))のデータを抽出するには以下のようにします。
[16]:
print(eq_result["X_ZN"])
<xarray.DataArray 'X_ZN' (X_ZN: 20)>
array([1.0e-10, 5.0e-02, 1.0e-01, 1.5e-01, 2.0e-01, 2.5e-01, 3.0e-01, 3.5e-01,
4.0e-01, 4.5e-01, 5.0e-01, 5.5e-01, 6.0e-01, 6.5e-01, 7.0e-01, 7.5e-01,
8.0e-01, 8.5e-01, 9.0e-01, 9.5e-01])
Coordinates:
* X_ZN (X_ZN) float64 1e-10 0.05 0.1 0.15 0.2 ... 0.75 0.8 0.85 0.9 0.95
次にまずy軸に対応する\(T\) = 800 KにおけるFCC_A1 相の相分率のデータを抽出するには以下のようにします。
[17]:
print(eq_result.NP.where(eq_result.Phase=='FCC_A1').sel(N=1, P=101325, T=800))
<xarray.DataArray 'NP' (X_ZN: 20, vertex: 3)>
array([[1. , nan, nan],
[1. , nan, nan],
[1. , nan, nan],
[1. , nan, nan],
[0.89739922, nan, nan],
[0.71825009, nan, nan],
[0.53910096, nan, nan],
[0.35995184, nan, nan],
[0.18080271, nan, nan],
[ nan, 0.00165358, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan],
[ nan, nan, nan]])
Coordinates:
N float64 1.0
P float64 1.013e+05
T float64 800.0
* X_ZN (X_ZN) float64 1e-10 0.05 0.1 0.15 0.2 ... 0.75 0.8 0.85 0.9 0.95
* vertex (vertex) int64 0 1 2
出力されたデータを見ると、相分率のNPはX_ZNとvertexの2つをcoordinatesとした2次元配列になっていることがわかります。
このままではグラフにプロットできないので、vertexについては和をとり1次元配列へ変換します。
[18]:
print(eq_result.NP.where(eq_result.Phase=='FCC_A1').sel(N=1, P=101325, T=800).sum('vertex'))
<xarray.DataArray 'NP' (X_ZN: 20)>
array([1. , 1. , 1. , 1. , 0.89739922,
0.71825009, 0.53910096, 0.35995184, 0.18080271, 0.00165358,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ])
Coordinates:
N float64 1.0
P float64 1.013e+05
T float64 800.0
* X_ZN (X_ZN) float64 1e-10 0.05 0.1 0.15 0.2 ... 0.75 0.8 0.85 0.9 0.95
このx、yデータをグラフにプロットするには以下のようにします。
[19]:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from pycalphad import Database, calculate, equilibrium, variables as v
from pycalphad.plot.utils import phase_legend
dbf = Database('alzn_mey.tdb')
comps = ['AL', 'ZN', 'VA']
phases = ['LIQUID', 'FCC_A1', 'HCP_A3']
eq_result = equilibrium(dbf, comps , phases, {v.X('ZN'):(0,1,0.05), v.T: (500, 1000, 100), v.P:101325}, output='HM')
X_ZN = eq_result["X_ZN"]
# Get the colors that map phase names to colors in the legend
#legend_handles, color_dict = phase_legend(phases)
fig = plt.figure(figsize=(6,4))
ax = fig.gca()
ax.scatter(X_ZN, eq_result.NP.where(eq_result.Phase=='FCC_A1').sel(N=1, P=101325, T=800).sum('vertex'), marker='.')
# Format the plot
ax.set_xlabel('X(Zn)')
ax.set_ylabel('Phase fraction')
ax.set_xlim((0, 1))
#ax.set_ylim((-60000, 0))
#ax.legend(handles=legend_handles, loc='lower right')
plt.show()
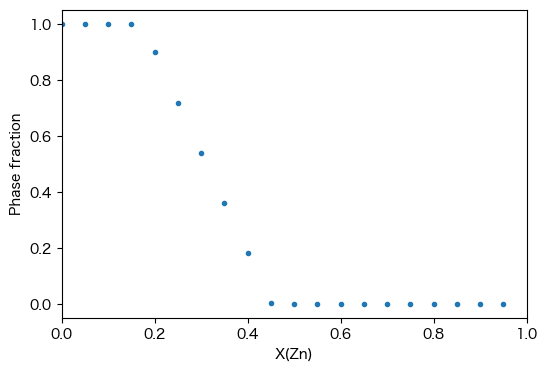
上の例に倣い、\(T\) = 800 Kにおける各相の相分率がZn濃度(X(ZN))に対して変化する図を作りましょう。
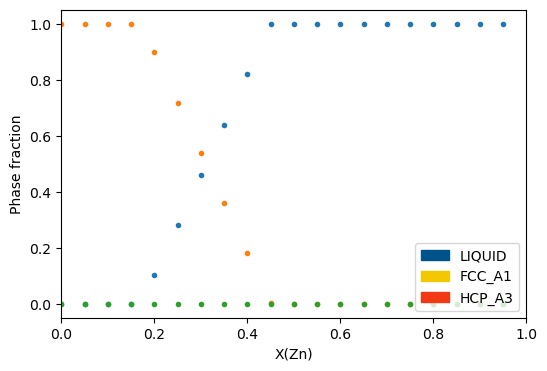
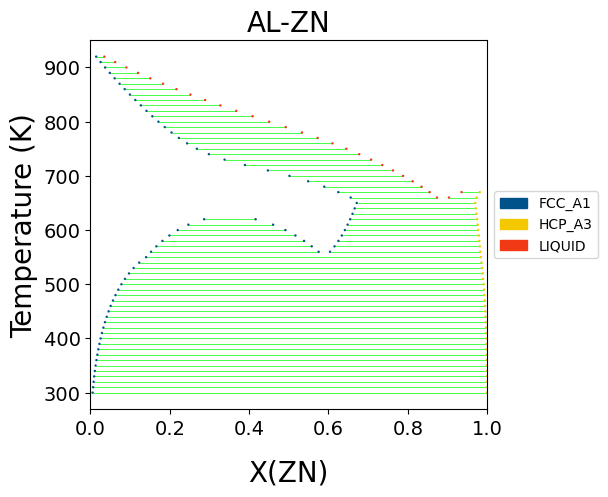
図からX(Zn) ~ 0.15までFCC_A1の単相、0.2 ~ X(Zn) ~ 0.45ではFCC_A1とLIQUIDの二相共存、0.45以上のX(Zn)領域ではLIQUIDの単相であることがわかります。これは前回作成した状態図と対応する結果となっていることが確認できます。
課題¶
Moodle上で提出する。
JupyterNotebook形式(*.ipynb)で提出する。
学籍番号、氏名を忘れずに記載する。
コードを実装するにあたって考えた過程や工夫したポイント、動作確認の方法等を記述してあれば評価時に考慮します。
moodleで配布した講義資料内にはAl-Mg_Zhong.tdb、NI_AL_DUPIN_2001.TDB、alfe_sei.TDB、nbre_liu.tdbが含まれている。
Al-Mg_Zhong.tdb:Al-Mg2元系の熱力学データベース
NI_AL_DUPIN_2001.TDB:Ni-Al2元系の熱力学データベース
alfe_sei.TDB:Al-Fe2元系の熱力学データベース
nbre_liu.tdb:Nb-Re2元系の熱力学データベース
alfe_sei.TDBを読み込み、\(T\) = 800 Kにおいて、各相の相分率がAl濃度に対して変化する図を作ってください。得られた計算結果が状態図と対応していることを確認し、文章で説明してください。
[ ]: