マルコフ連鎖モンテカルロ (MCMC)

　ESPEI は、相境界データに対する熱力学パラメータの最適化と不確定性の定量化を行うことができます。熱力学パラメータの最適化と不確定性の定量化には、マルコフ連鎖モンテカルロ法(MCMC) が使用されています。既存の熱力学データベースに加えてESPEIによって生成されたデータベースなど、任意の CALPHAD データベースを使用することができます。

　ESPEIは pycalphad でサポートされているすべての熱力学モデルをサポートしています。またユーザー定義の熱力学モデルも、pycalphadと互換性がある場合には、ESPEIのコードに変更を加えずに使用することができます。

　ESPEI に使用できる最小限の設定ファイルを示しています。データベースと反復回数を設定することが必要です。ここではパラメータ選択で作成したデータベースを指定しています。

system:
  phase_models: phases.json
  datasets: input-data/run
output:
  output_db:  mcmc.tdb
  verbosity:  2
mcmc:
  iterations: 100
  input_db: dft-aicc_penalty.tdb

インプットファイル (YAML)

　フィッティング手順を記述し、ハイパーパラメータの調整をするYAMLファイルです。詳細については、YAML Input Schemaを参照してください。

デフォルトでは、ESPEIはdaskパッケージを使用して並列実行されます。ローカルで実行する場合は、daskの設定が必要になる場合があります。

　通常では限られたリソースを使用することになるため、精度とストレージ容量に関して妥協が必要になることがあります。MCMCシミュレーションを実行するための設定は以下の通りです（mcmc_settings.yaml）。

system:
  phase_models: Cr-Ni_phases.json
  datasets: input-data
  tags:
    dft:
      excluded_model_contributions: ['idmix', 'mag']
      weight: 0.1
    nomag:
      excluded_model_contributions: ['mag']
    estimated-entropy:
      excluded_model_contributions: ['idmix', 'mag']
      weight: 0.1
output:
  output_db:  mcmc.tdb
  verbosity:  2
  tracefile:  Cr-Ni-trace_100.npy
  probfile:   Cr-Ni-lnprob_100.npy
  logfile:    Cr-Ni-mcmc_100.log
mcmc:
  iterations: 100
  save_interval: 1
  scheduler: null   # no parallelization
  input_db: mcmc-start.tdb  # same as our generated-aicc.tdb
  chains_per_parameter: 2
  data_weights:
    ZPF: 40.0
    SM: 0.1

output:

　出力は、最適パラメータと、トレース（すべてのチェーンと反復におけるパラメータを含む）と対数尤度を含む emcee.EnsembleSampler オブジェクトです。

tracefile：

　トレースを出力するファイル名を指定します。配列の形状は（チェーン数、反復回数、パラメータ数）です。

probfile:

　対数確率を出力するファイル名を指定します。配列の形状は（チェーン数、反復回数）です。

　トレースと対数確率の配列は事前に割り当てられ、ゼロが埋め込まれています。このため、2000 回の MCMC 反復を選択したが 1500 回しか実行されなかった場合は、最後の 500 個の値はすべて 0 になります。ファイル名はユニークである必要があり、既に存在する場合にはエラーとなります。ファイルを出力したくない場合には、null を入力してください。

mcmc:

　emceeを使用して、マルコフ連鎖モンテカルロを制御します。MCMCフィッティングを実行するには、最適化するパラメータを指定する必要があります。これには、generate_parameters のステップを含めるか、mcmc.input_db にpycalphadデータベースを設定することで取得できます。

　データベースからのパラメータを使用することを選択した場合は、それが最初の MCMC 実行であるか、または前回の実行から継続しているか (restart) に基づいて設定をさらに制御できます。

iterations:

　反復回数。上の例ではMCMCシミュレーションを100回実行します。

prior:

　パラメータの事前分布。事前分布の詳細については、事前分布の指定を参照してください。

scheduler:

　並列化に使用するスケジューラ。dask、null、またはdask-distributedによって作成されたJSONスケジューラファイルへのパスのいずれかを選択できます。dask を選択すると、cores を通じて使用するコア数を選択できます。nullを選択すると、並列スケジューラは使用されません。これはデバッグに役立ちます。JSONスケジューラファイルへのパスを渡すと、スケジューラによって設定されたリソースが使用されます。JSONファイルスケジューラは、dask-mpiコマンドを使用してMPIクラスター上でスケジューラを起動できるため、非常に便利です。詳細については、代替スケジューラのページを参照してください。

restart_trace:

　MCMC計算を実行すると、すべてのチェーンの位置と履歴を記述したトレースファイルが作成されます。このrestart_traceにトレースファイル（chain.npyなど）を設定することで、MCMC計算を再開することができます。再開する場合は、使用したデータベースファイル (input_db)も同様に指定する必要があります。

chains_per_parameter:

　MCMC 計算で使用するチェーンの数を、パラメータ数の整数倍として指定します。このパラメータは、最初のMCMC実行のみ使用し、計算を再開する場合のチェーン数は以前に選択した数に固定されます。emceeのEnsemble samplersは、p個のフィッティングパラメータに対して少なくとも2*p個のチェーンを必要とします。chains_per_parameter = 2 の場合、フィッティングするパラメータが10個ある場合のチェーン数は20です。chains_per_parameter の値は偶数でなければなりません。

data_weights:

　ゼロ相分率（ZPF）、活量（ACR）、様々な誤差といった各データに重み付けが可能です。これらの重み\(\omega\)は、各データの標準偏差を以下のように修正します。

\begin{equation} \sigma = \frac{\sigma_{initial}}{\omega} \end{equation}

　MCMCのすべてのオプションは、YAML Input Schemaで説明されています。パラメータ生成と比べて、オプションはより広範囲にわたります。

MCMCの実行

　MCMCの実行にはrun_espeiを使用します。run_espeiは、MCMCにより最適化されたデータベースdbf_mcmcと、サンプル毎のデータを含むsamplerを出力します。

import yaml
from espei import run_espei
from pycalphad import Database, binplot, equilibrium, variables as v

with open('mcmc_settings.yaml') as fp:
    mcmc_settings = yaml.safe_load(fp)

dbf_mcmc, sampler = run_espei(mcmc_settings)

　samplerの出力は、trace（emcee ではこれをchainと呼びます）とlnprob（対数確率）です。

• traceは (chains, iterations, parameters) の形をとります。

• lnprobは (chains, iterations) の形をとります。

　MCMCの結果は、NumPy配列として出力ファイルに保存されます。ファイル名はrun_mcmc.yamlファイルで設定します。デフォルトはそれぞれtrace.npyとlnprob.npyです。

trace = sampler.chain
lnprob = sampler.lnprobability

print(f"Trace shape:           {trace.shape}")
print(f"Log-probability shape: {lnprob.shape}")

Trace shape:           (20, 100, 10)
Log-probability shape: (20, 100)

　MCMC シミュレーションの結果、状態図がどのようになったかを確認します。まずmcmc-start.tdbをdbf_startとして読み込み図示します。

from espei.plot import dataplot
from espei.datasets import recursive_glob, load_datasets

# load our JSON datasets into an in-memory database
datasets = load_datasets(recursive_glob('input-data', '*.json'))

dbf_start = Database('mcmc-start.tdb')
comps = ['CR', 'NI']
phases = ['FCC_A1', 'BCC_A2', 'LIQUID']
conds = {v.N: 1.0, v.P: 101325, v.T: (300, 2300, 20), v.X('NI'): (0, 1, 0.02)}
ax = binplot(dbf_start, comps, phases, conds)
dataplot(comps, phases, conds, datasets, ax=ax)

<Axes: title={'center': 'CR-NI'}, xlabel='X(NI)', ylabel='Temperature (K)'>

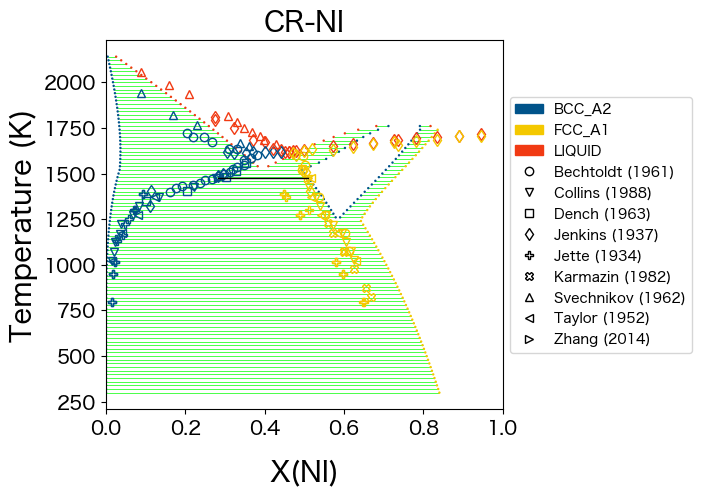
　次にMCMC シミュレーションにより得られたdbf_mcmcの結果を図示します。

comps = ['CR', 'NI']
phases = ['FCC_A1', 'BCC_A2', 'LIQUID']
conds = {v.N: 1.0, v.P: 101325, v.T: (300, 2300, 20), v.X('NI'): (0, 1, 0.02)}
ax = binplot(dbf_mcmc, comps, phases, conds)
dataplot(comps, phases, conds, datasets, ax=ax)

<Axes: title={'center': 'CR-NI'}, xlabel='X(NI)', ylabel='Temperature (K)'>

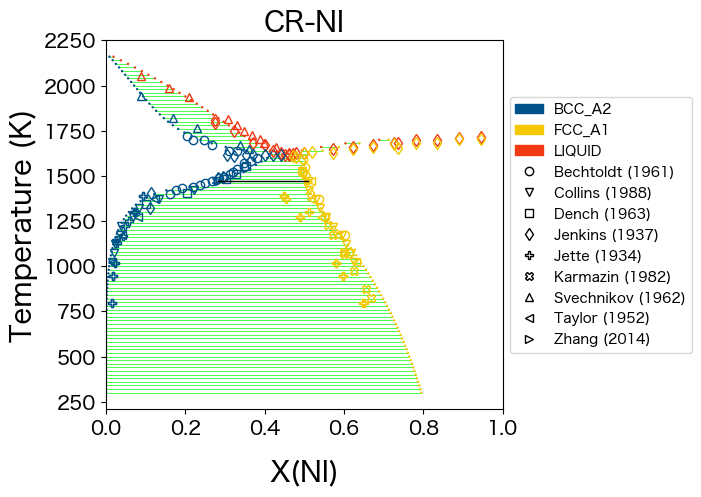
　20 チェーンにわたる MCMC の 100 回の反復で、相図に劇的な改善が見られています。

　ESPEIを使用すると、熱力学データベースをユーザーによる操作をほとんど必要とせずに簡単に再最適化できるため、後からデータを追加してデータベースを再最適化する際にも、計算時間のみを消費するだけで済みます。実際、第一原理から直接得られるデータベースではなく、推定値から得られた既存のデータベースを出発点として使用し、新しいデータに合わせてデータベースを簡単に修正することができます。

MCMC データの解析

　MCMCの実行が終了したら結果を分析します。通常、不確実性の定量化を行うのに十分なサンプルを持つ完全に収束した MCMC シミュレーションには、数百から数千の計算が必要になります。40個のチェーンをサンプリングし、1000回の反復処理を行い、パラメータ空間で合計40,000個のサンプルを取得した場合、2015年製MacBook Pro（2.2GHz Intel i7）の6コアで実行するのには3.5時間かかっています。

　MCMCの結果は、NumPy配列として出力ファイルに保存されます。ファイル名はrun_mcmc.yamlファイルで設定します。デフォルトはそれぞれtrace.npyとlnprob.npyです。trace.npyには、すべてのチェーンと反復で提案されたすべてのパラメータ（トレース）が含まれます。lnprob.npyには、すべてのチェーンと反復で計算されたすべての対数確率（慣例により負の数）が含まれます。

import numpy as np
from espei.analysis import truncate_arrays

# load our trace and lnprob files to use in later analysis steps
trace = np.load('Cr-Ni-trace_100.npy')
lnprob = np.load('Cr-Ni-lnprob_100.npy')

trace, lnprob = truncate_arrays(trace, lnprob)

print(trace.shape)
print(lnprob.shape)

(20, 100, 10)
(20, 100)

　truncate_arraysは、traceとlnprobから空データを除くために使用します。

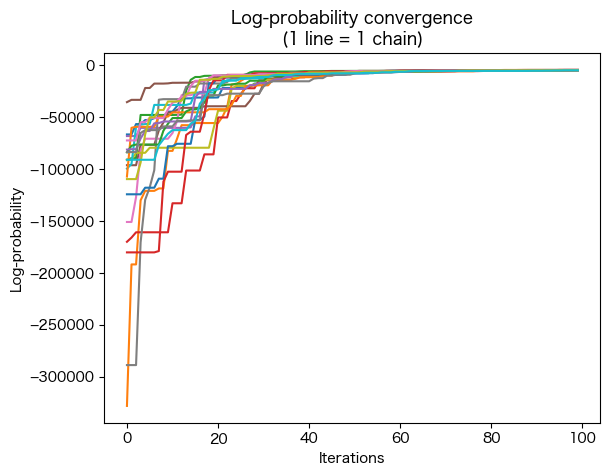
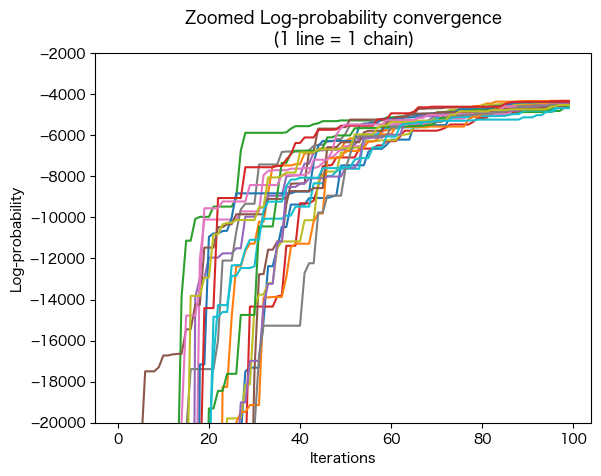
収束性の確認 (lnprob)

　収束性は、すべてのchainのlnprobが、iterationsの関数としてどのように変化したかを見ることによって、定性的に評価することができます。

　収束性の評価に役立つ方法はいくつか存在しますが、ESPEI で使用されるようなアンサンブル MCMC 法には独立したchainがないため、複数の独立したchainのための方法は注意して使用する必要があります。

　lnprobは (chains, iterations) の形をとっているため、横軸をiterationsで作図するにはlnprob.Tとして転置して使用します。

import matplotlib.pyplot as plt
plt.plot(lnprob.T)
plt.title('Log-probability convergence\n(1 line = 1 chain)')
plt.xlabel('Iterations')
plt.ylabel('Log-probability')

plt.figure()
plt.plot(lnprob.T)
plt.title('Zoomed Log-probability convergence\n(1 line = 1 chain)')
plt.xlabel('Iterations')
plt.ylabel('Log-probability')
plt.ylim(-20000, -2000)

(-20000.0, -2000.0)

パラメータ変化の確認 (trace)

　parameter毎のchainが、chain全体でどのように変化するかを見ると、

• 特定のchainが他のchainから分岐しているかどうか

• 複数のモードが探索されているかどうか

• またはparameterの分布が互いに対してどの程度広いか

がわかります。

　以下の例ではparameter_idx = 5としてパラメータの作図をしています。traceは (chains, iterations,parameters) の形をとっているため、横軸をiterationsで作図するには、

trace[..., parameter_idx].T

として転置して使用します。chainsとiterationsの指定は...で省略されています。

# index of parameter of interest within the chain
# could be looped to produce figures for all parameters
parameter_idx = 5

num_chains = trace.shape[0]
ax = plt.figure().gca()
ax.set_xlabel('Iterations')
ax.set_ylabel('Parameter value')
ax.plot(trace[..., parameter_idx].T)
ax.set_title('Parameter Convergence')

Text(0.5, 1.0, 'Parameter Convergence')

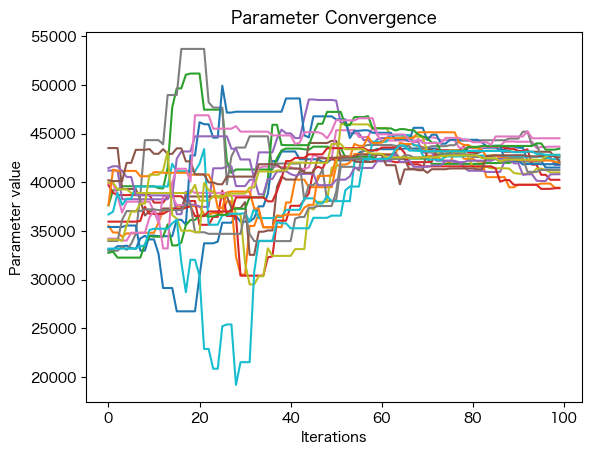
　各ラインはアンサンブル内の 1 つのchainに対応します。

　以下の例ではparameterをループで変化させて全てのパラメータの作図をしています。

import matplotlib.pyplot as plt
import numpy as np
from espei.analysis import truncate_arrays

trace = np.load('Cr-Ni-trace_100.npy')
lnprob = np.load('Cr-Ni-lnprob_100.npy')
trace, lnprob = truncate_arrays(trace, lnprob)

num_chains = trace.shape[0]
num_parameters = trace.shape[2]
iterations = np.arange(1,trace.shape[1]+1)
fig, axs = plt.subplots(nrows=num_parameters, gridspec_kw=dict(hspace=0.4), figsize=(4, 3*num_parameters))
for parameter in range(num_parameters):
    ax = axs[parameter]
    ax.set_xlabel('Iterations')
    ax.set_ylabel('Parameter value')
    ax.plot(iterations, trace[..., parameter].T)
fig.show()

/var/folders/db/44nwhkz57zd4pk88j94pvdtc0000gn/T/ipykernel_97771/807957251.py:18: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
  fig.show()

最適なパラメータセットの取得

　MCMC シミュレーションでは多くのサンプルを取得しますが、optimal_parameters(trace, lnprob) を使用して最適なパラメータセットを取得することができます。

　さらにdatabase.symbols.update を使用して、データベース内の変数 ($ \mathrm{VV0001} $、…) を更新することができます。

from espei.utils import database_symbols_to_fit, optimal_parameters
import copy
from pycalphad import Database

# make an in-memory copy of the database because updating the
# symbols with the optimal solutions will erase the old ones
dbf_start = Database('mcmc-start.tdb')
dbf_opt = copy.deepcopy(dbf_start)

# Find the optimal parameters and replace the values in the symbols dictionary
opt_params = dict(zip(database_symbols_to_fit(dbf_opt), optimal_parameters(trace, lnprob)))
dbf_opt.symbols.update(opt_params)

　変数を更新すると古いものが消去されるため、まずデータベース(dbf_start)のコピー(dbf_opt)を作成します。次に最適なパラメータをoptimal_parameters(trace, lnprob)で読み込み、変数の値を置き換えます。

dbf_optを使用して作図すると、読み込んだデータベース(mcmc-start.tdb)ではなく、MCMCの最適パラメータがdbf_optに取得できていることがわかります。

from espei.plot import dataplot
from espei.datasets import recursive_glob, load_datasets
from pycalphad import binplot, variables as v

# load our JSON datasets into an in-memory database
datasets = load_datasets(recursive_glob('input-data', '*.json'))

# plot the phase diagram
comps = ['CR', 'NI']
phases = ['FCC_A1', 'BCC_A2', 'LIQUID']
conds = {v.N: 1.0, v.P: 101325, v.T: (300, 2300, 20), v.X('NI'): (0, 1, 0.02)}

ax = binplot(dbf_opt, comps, phases, conds)
dataplot(comps, phases, conds, datasets, ax=ax)

<Axes: title={'center': 'CR-NI'}, xlabel='X(NI)', ylabel='Temperature (K)'>

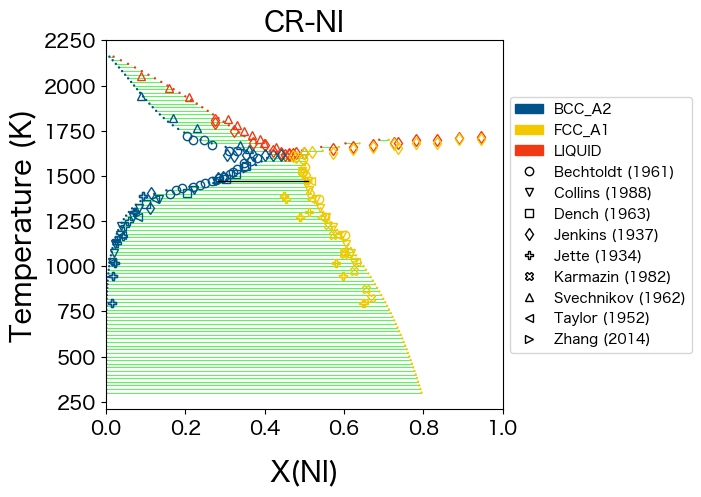
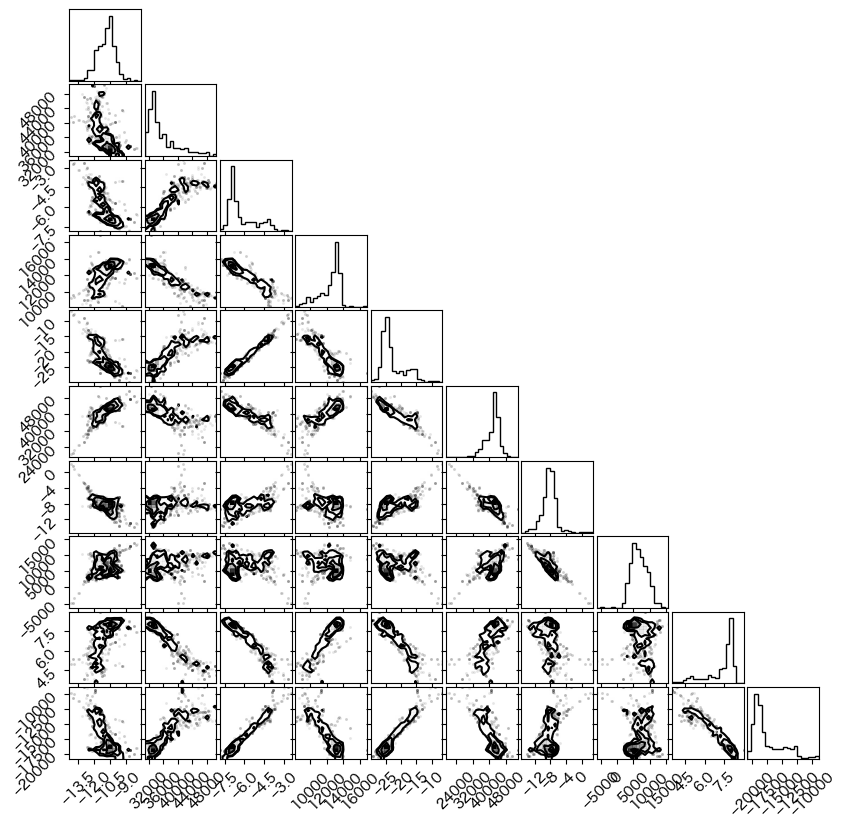
MCMC Corner Plots

　Corner Plotsでは、各パラメータの値の分布が対角線に沿ってプロットされます。また、各パラメータ間の共分散が対角線の下にプロットされます。共分散が円形に近いほどパラメータ間に相関がないことを意味し、細長い形状は2つのパラメータ間に相関があることを示します。

　単一相内、または平衡状態の相間において Calphad モデルの一部のパラメータには、強く相関したパラメータが含まれることが予想されます。この場合、1 つのパラメータを増加させながら別のパラメータを減少させると同様の尤度が得られます。MCMC法を最初に実行する場合には、このような相関の大きい初期パラメータのいくつかを破棄します。

　生成される図は比較的小さい figsize=(8,8) で、ページに収まりやすいように設定されています。corner.corner に fig 引数を渡さずに図を大きくすると、より読みやすくなります（corner.corner に fig を渡さないで試してください）。

import matplotlib.pyplot as plt
import numpy as np
import corner

trace = np.load('Cr-Ni-trace_100.npy')

# the following lines are optional, but useful if your traces are not full
# (i.e. your MCMC runs didn't run all their steps)
# from espei.analysis import truncate_arrays
# lnprob = np.load('lnprob.npy')
# trace, lnprob = truncate_arrays(trace, lnprob)

#burn_in_iterations = 500  # number of samples of burn-in to discard
burn_in_iterations = 10  # number of samples of burn-in to discard
print("(# chains, # iterations, # parameters)")
print(f"Trace shape: {trace.shape}")
print(f"Trace shape after burn-in: {trace[:, burn_in_iterations:, :].shape}")

# flatten the along the first dimension containing all the chains in parallel
fig = plt.figure(figsize=(8,8))  # figures for corner cannot have axes
corner.corner(trace[:, burn_in_iterations:, :].reshape(-1, trace.shape[-1]), fig=fig)
fig.show()

(# chains, # iterations, # parameters)
Trace shape: (20, 100, 10)
Trace shape after burn-in: (20, 90, 10)

/var/folders/db/44nwhkz57zd4pk88j94pvdtc0000gn/T/ipykernel_33047/3777355005.py:22: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
  fig.show()

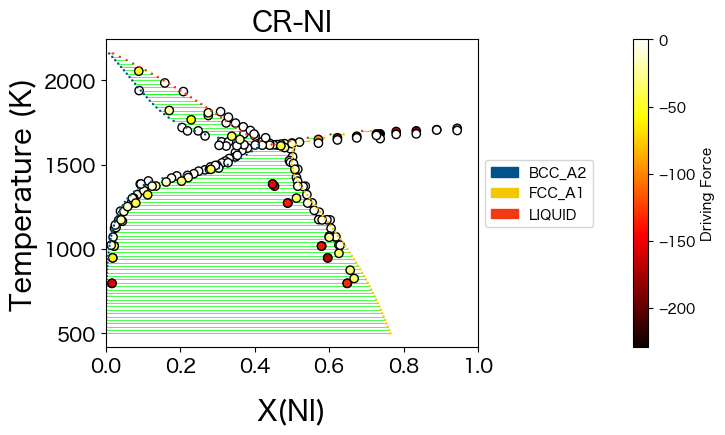
Plot ZPF Driving Forces

　どのZPFデータ（相境界データ）が尤度に大きな駆動力（ばらつき）を与えているか診断することができます。これらの駆動力は、フィッティングに関して重み付けされていないことに注意してください。重みは、各駆動力の対数尤度を計算する際に適用される（つまりばらつきの評価に使用される？）ためです。

import numpy as np
import matplotlib.pyplot as plt
from pycalphad import Database, binplot, variables as v
from pycalphad.core.utils import extract_parameters
from espei.datasets import load_datasets, recursive_glob
from espei.error_functions.zpf_error import get_zpf_data, calculate_zpf_driving_forces

dbf = Database("mcmc.tdb")
comps = ["CR", "NI", "VA"]
phases = list(dbf.phases.keys())
indep_comp_cond = v.X("NI")  # binary assumed
conditions = {v.N: 1, v.P: 101325, v.T: (500, 2200, 20), indep_comp_cond: (0, 1, 0.01)}
parameters = {}  # e.g. {"VV0001": 10000.0}, if empty, will use the current database parameters

# Get the datasets, construct ZPF data and compute driving forces
# Driving forces and weights are ragged 2D arrays of shape (len(zpf_data), len(vertices in each zpf_data))
datasets = load_datasets(recursive_glob("input-data"))
zpf_data = get_zpf_data(dbf, comps, phases, datasets, parameters=parameters)
param_vec = extract_parameters(parameters)[1]
driving_forces, weights = calculate_zpf_driving_forces(zpf_data, param_vec)

# Construct the plotting compositions, temperatures and driving forces
# Each should have len() == (number of vertices)
# Driving forces already have the vertices unrolled so we can concatenate directly
Xs = []
Ts = []
dfs = []
for data, data_driving_forces in zip(zpf_data, driving_forces):
    # zpf_data have (ragged) shape (len(datasets), len(phase_regions), len(vertices))
    # while driving_forces have (ragged) shape (len(datasets), len(vertices)), concatenating along the phase regions dimension
    # so we need an offset to account for phase veritices from previous phase regions
    driving_force_offset = 0
    for phase_region in data["phase_regions"]:
        for vertex, df in zip(phase_region.vertices, data_driving_forces[driving_force_offset:]):
            driving_force_offset += 1
            comp_cond = vertex.comp_conds
            if vertex.has_missing_comp_cond:
                # No composition to plot
                continue
            dfs.append(df)
            Ts.append(phase_region.potential_conds[v.T])
            # Binary assumptions here
            assert len(comp_cond) == 1
            if indep_comp_cond in comp_cond:
                Xs.append(comp_cond[indep_comp_cond])
            else:
                # Switch the dependent and independent component
                Xs.append(1.0 - tuple(comp_cond.values())[0])

# Plot the phase diagram with driving forces
fig, ax = plt.subplots(dpi=100, figsize=(8,4))
binplot(dbf, comps, phases, conditions, plot_kwargs=dict(ax=ax), eq_kwargs={"parameters": parameters})
sm = plt.cm.ScalarMappable(cmap="hot")
sm.set_array(dfs)
ax.scatter(Xs, Ts, c=dfs, cmap="hot", edgecolors="k")
fig.colorbar(sm, ax=ax, pad=0.25, label="Driving Force")
fig.show()

/var/folders/db/44nwhkz57zd4pk88j94pvdtc0000gn/T/ipykernel_97771/2969301569.py:57: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
  fig.show()